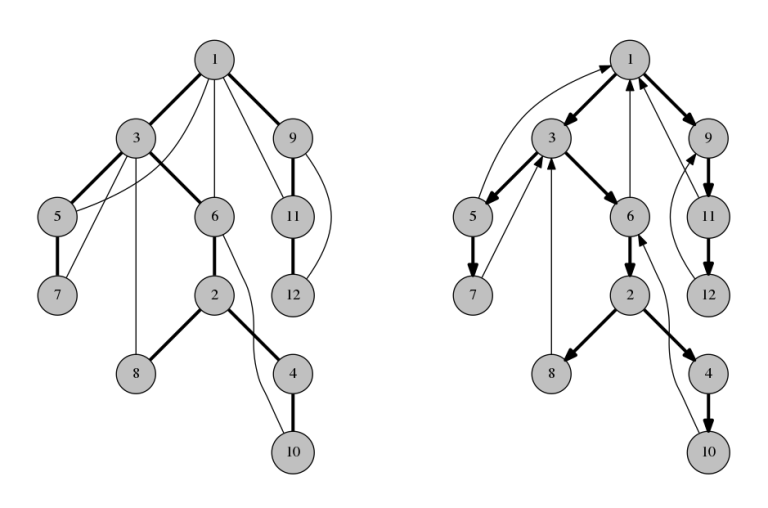
В этой статье рассмотрены основные применения обхода в глубину: топологическая сортировка, нахождение компонент сильной связности, решение задачи 2-SAT, нахождение мостов и точек сочленения, а также построение эйлерова пути и цикла в графе.
Поиском в глубину (англ. depth-first search, DFS) называется рекурсивный алгоритм обхода дерева или графа, начинающий в корневой вершине (в случае графа её может быть выбрана произвольная вершина) и рекурсивно обходящий весь граф, посещая каждую вершину ровно один раз.
const int maxn = 1e5;
bool used[maxn]; // тут будем отмечать посещенные вершины
void dfs(int v) {
used[v] = true;
for (int u : g[v])
if (!used[u])
dfs(v);
}Немного его модифицируем, а именно будем сохранять для каждой вершины, в какой момент мы в неё вошли и в какой вышли — соответствующие массивы будем называть \(tin\) и \(tout\).
Как их заполнить: заведем таймер, отвечающий за «время» на текущем состоянии обхода, и будем инкрементировать его каждый раз, когда заходим в новую вершину:
int tin[maxn], tout[maxn];
int t = 0;
void dfs(int v) {
tin[v] = t++;
for (int u : g[v])
if (!used[u])
dfs(u);
tout[v] = t; // иногда счетчик тут тоже увеличивают
}У этих массивов много полезных свойств:
Эти свойства часто бывают полезными в задачах на деревья.
Определение. Мостом называется ребро, при удалении которого связный неориентированный граф становится несвязным.
Определение. Точкой сочленения называется врешина, при удалении которой связный неориентированный граф становится несвязным.
Пример задачи, где их интересно искать: дана топология сети (компьютеры и физические соединения между ними) и требуется установить все единые точки отказа — узлы и связи, без которых будут существовать два узла, между которыми не будет пути.
Наивный алгоритм поочередного удаления каждого ребра \((u, v)\) и проверки наличия пути \(u \leadsto v\) потребует \(O(m^2)\) операций. Чтобы научиться находить мосты быстрее, сначала сформулируем несколько утверждений, связанных с обходом в глубину.
Запустим DFS из произвольной вершины. Введем новые виды рёбер:
Прямые рёбра — те, по которым были переходы в dfs.
Обратные рёбра — то, по которым не было переходов в dfs.
Заметим, что никакое обратное ребро \((u, v)\) не может являться мостом: если его удалить, то всё равно будет существовать какой-то путь от \(u\) до \(v\), потому что подграф из прямых рёбер является связным деревом.
Значит, остается только проверить все прямые рёбра. Это уже немного лучше — такой алгоритм будет работать за \(O(n m)\).
Сооптимизировать его до линейного времени (до одного прохода dfs) поможет замечание о том, что обратные рёбра могут вести только «вверх» — к какому-то предку в дереве обхода графа, но не в другие «ветки» — иначе бы dfs увидел это ребро раньше, и оно было бы прямым, а не обратным.
Тогда, чтобы определить, является ли прямое ребро \(v \to u\) мостом, мы можем воспользоваться следующим критерием: глубина \(h_v\) вершины \(v\) меньше, чем минимальная глубина всех вершин, соединенных обратным ребром с какой-либо вершиной из поддерева \(u\).
Для ясности, обозначим эту величину как \(d_u\), которую можно считать во время обхода по следующей формуле:
\[ d_v = \min \begin{cases} h_v, &\\ d_u, &\text{ребро } (v \to u) \text{ прямое} \\ h_u, &\text{ребро } (v \to u) \text{ обратное} \end{cases} \]
Если это условие (\(h_v < d_u\)) не выполняется, то существует какой-то путь из \(u\) в какого-то предка \(v\) или саму \(v\), не использующий ребро \((v, u)\), а в противном случае — наоборот.
const int maxn = 1e5;
bool used[maxn];
int h[maxn], d[maxn];
void dfs(int v, int p = -1) {
used[u] = true;
d[v] = h[v] = (p == -1 ? 0 : h[p] + 1);
for (int u : g[v]) {
if (u != p) {
if (used[u]) // если рябро обратное
d[v] = min(d[v], h[u]);
else { // если рябро прямое
dfs(u, v);
d[v] = min(d[v], d[u]);
if (h[v] < d[v]) {
// ребро (v, u) -- мост
}
}
}
}
}Примечание. Более известен алгоритм, вместо глубин вершин использующий их \(tin\), но автор считает его чуть более сложным для понимания.
Задача поиска точек сочленения не сильно отличается от задачи поиска мостов.
Вершина \(v\) является точкой сочленения, когда из какого-то её ребёнка \(u\) нельзя дойти до её предка, не используя ребро \((v, u)\). Для конкретного прямого ребра \(v \to u\) этот факт можно проверить так: \(h_v \leq d_u\) (теперь нам нам достаточно нестрогого неравенства, так как если из вершины можно добраться до нее самой, то она все равно будет точкой сочленения).
Используя этот факт, можно оставить алгоритм практически прежним — нужно проверить этот критерий для всех прямых рёбер \(v \to u\):
void dfs(int v, int p = -1) {
used[u] = 1;
d[v] = h[v] = (p == -1 ? 0 : h[p] + 1);
int children = 0; // случай с корнем обработаем отдельно
for (int u : g[u]) {
if (u != p) {
if (used[u])
d[v] = min(d[v], h[u]);
else {
dfs(u, v);
d[v] = min(d[v], d[u]);
if (dp[v] >= tin[u] && p != -1) {
// u -- точка сочленения
}
children++;
}
}
}
if (p == -1 && children > 1) {
// v -- корень и точка сочленения
}
}Единственный крайний случай — это корень, так как в него мы по определению войдём раньше других вершин. Но фикс здесь очень простой — достаточно посмотреть, было ли у него более одной ветви в обходе (если корень удалить, то эти поддеревья станут несвязными между собой).
Задача топологической сортировки графа звучит так: дан ориентированный граф, нужно упорядочить его вершины в массиве так, чтобы все графа рёбра вели из более ранней вершины в более позднюю.
Это может быть полезно, например, при планировании выполнения связанных задач: вам нужно одеться, в правильном порядке надев шорты (1), штаны (2), ботинки (3), подвернуть штаны (4) — как хипстеры — и завязать шнурки (5).
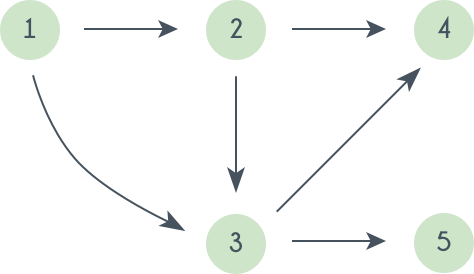
Во-первых, сразу заметим, что граф с циклом топологически отсортировать не получится — как ни располагай цикл в массиве, все время идти вправо по ребрам цикла не получится.
Во-вторых, верно обратное. Если цикла нет, то его обязательно можно топологически отсортировать — сейчас покажем, как.
Заметим, что вершину, из которой не ведет ни одно ребро, можно всегда поставить последней, а такая вершина в ациклическом графе всегда есть (иначе можно было бы идти по обратным рёбрам бесконечно). Из этого сразу следует конструктивное доказательство: будем итеративно класть в массив вершину, из которой ничего не ведет, и убирать ее из графа. После этого процесса массив надо будет развернуть.
Этот алгоритм проще реализовать, обратив внимание на времена выхода вершин в dfs. Вершина, из которой мы выйдем первой — та, у которой нет новых исходящих ребер. Дальше мы будем выходить только из тех вершин, которые если имеют исходящие ребра, то только в те вершины, из которых мы уже вышли.
Следовательно, достаточно просто выписать вершины в порядке выхода из dfs, а затем полученный список развернуть, и мы получим какую-то из корректных топологических сортировок.
Мы только что научились топологически сортировать ациклические графы. А что же делать с циклическими графами? В них тоже иногда требуется найти какую-то структуру.
Для этого можно ввести понятие сильной связности.
Определение. Две вершины ориентированного графа связаны сильно (англ. strongly connected), если существует путь из одной в другую и наоборот. Иными словами, они обе лежат в каком-то цикле.
Понятно, что такое отношение транзитивно: если \(a\) и \(b\) сильно связны, и \(b\) и \(c\) сильно связны, то \(a\) и \(c\) тоже сильно связны. Поэтому все вершины распадаются на компоненты сильной связности — такое разбиение вершин, что внутри одной компоненты все вершины сильно связаны, а между вершинами разных компонент сильной связности нет.
Самый простой пример сильно-связной компоненты — это цикл. Но это может быть и полный граф, или сложное пересечение нескольких циклов.
Часто рассматривают граф, составленный из самих компонент сильной связности, а не индивидуальных вершин. Очевидно, такой граф уже будет ациклическим, и с ним проще работать. Задачу о сжатии каждой компоненты сильной связности в одну вершину называют конденсацией графа, и её решение мы сейчас опишем.
Если мы знаем, какие вершины лежат в каждой компоненте сильной связности, то построить граф конденсации несложно: дальше нужно лишь провести некоторые манипуляции со списками смежности. Поэтому сразу сведем исходную задачу к нахождению самих компонент.
Лемма. Запустим dfs. Пусть \(A\) и \(B\) — две различные компоненты сильной связности, и пусть в графе конденсации между ними есть ребро \(A \to B\). Тогда:
\[ \max\limits_{a \in A}(tout_a) > \max\limits_{b\in B}(tout_b) \]
Доказательство. Рассмотрим два случая, в зависимости от того, в какую из компонент dfs зайдёт первым.
Пусть первой была достигнута компонента \(A\), то есть в какой-то момент времени dfs заходит в некоторую вершину \(v\) компоненты \(A\), и при этом все остальные вершины компонент \(A\) и \(B\) ещё не посещены. Но так как по условию в графе конденсаций есть ребро \(A \to B\), то из вершины \(v\) будет достижима не только вся компонента \(A\), но и вся компонента \(B\). Это означает, что при запуске из вершины \(v\) обход в глубину пройдёт по всем вершинам компонент \(A\) и \(B\), а, значит, они станут потомками по отношению к \(v\) в дереве обхода, и для любой вершины \(u \in A \cup B, u \ne v\) будет выполнено \(tout_v] > tout_u\), что и утверждалось.
Второй случай проще: из \(B\) по условию нельзя дойти до \(A\), а значит, если первой была достигнута \(B\), то dfs выйдет из всех её вершин ещё до того, как войти в \(A\).
Из этого факта следует первая часть решения. Отсортируем вершины по убыванию времени выхода (как бы сделаем топологическую сортировку, но на циклическом графе). Рассмотрим компоненту сильной связности первой вершины в сортировке. В эту компоненту точно не входят никакие рёбра из других компонент — иначе нарушилось бы условие леммы, ведь у первой вершины \(tout\) максимальный . Поэтому, если развернуть все рёбра в графе, то из этой вершины будет достижима своя компонента сильной связности \(C^\prime\), и больше ничего — если в исходном графе не было рёбер из других компонент, то в транспонированном не будет ребер в другие компоненты.
После того, как мы сделали это с первой вершиной, мы можем пойти по топологически отсортированному списку дальше и делать то же самое с вершинами, для которых компоненту связности мы ещё не отметили.
vector<int> g[maxn], t[maxn];
vector<int> order;
bool used[maxn];
int component[maxn];
int cnt_components = 0;
// топологическая сортировка
void dfs1(int v) {
used[v] = true;
for (int u : g[v]) {
if (!used[u])
dfs1(u);
order.push_back(v);
}
// маркировка компонент сильной связности
void dfs2(int v) {
component[v] = cnt_components;
for (int u : t[v])
if (cnt_components[u] == 0)
dfs2(u);
}
// в содержательной части main:
// транспонируем граф
for (int v = 0; v < n; v++)
for (int u : g[v])
t[u].push_back(v);
// запускаем топологическую сортировку
for (int i = 0; i < n; i++)
if (!used[i])
dfs1(i);
// выделяем компоненты
reverse(order.begin(), order.end());
for (int v : order)
if (component[v] == 0)
dfs2(v);TL;DR:
Сортируем вершины в порядке убывания времени выхода.
Проходимся по массиву вершин в этом порядке, и для ещё непомеченных вершин запускаем dfs на транспонированном графе, помечающий все достижимые вершины номером новой компонентой связности.
После этого номера компонент связности будут топологически отсортированы.
Ликбез. Конъюнкция — это «правильный» термин для логического «И» (обозначается \(\wedge\) или &). Конъюкция возвращает true тогда и только тогда, когда обе переменные true.
Ликбез. Дизъюнкция — это «правильный» термин для логического «ИЛИ» (обозначается \(\vee\) или |). Дизъюнкция возвращает false тогда и только тогда, когда обе переменные false.
Рассмотрим конъюнкцию дизъюнктов, то есть «И» от «ИЛИ» от каких-то перемений или их отрицаний. Например, такое выражение:
(a | b) & (!c | d) & (!a | !b)Если буквами: (А ИЛИ B) И (НЕ C ИЛИ D) И (НЕ A ИЛИ НЕ B).
Можно показать, что любую логическую формулу можно представить в таком виде.
Задача satisfiability (SAT) заключается в том, чтобы найти такие значения переменных, при которых выражение становится истинным, или сказать, что такого набора значений нет. Для примера выше такими значениями являются a=1, b=0, c=0, d=1 (убедитесь, что каждая скобка стала true).
В случае произвольных формул эта задача быстро не решается. Мы же хотим решить её частный случай — когда у нас в каждой скобке ровно две переменные (2-SAT).
Казалось бы — причем тут графы? Заметим, что выражение \(a \, | \, b\) эквивалентно \(!a \rightarrow b \,| \, !b \rightarrow a\). Здесь «\(\rightarrow\)» означает импликацию («если \(a\) верно, то \(b\) тоже верно»). С помощью это подстановки приведем выражение к другому виду — импликативному.
Затем построим граф импликаций: для каждой переменной в графе будет по две вершины, (обозначим их через \(x\) и \(!x\)), а рёбра в этом графе будут соответствовать импликациям.
Заметим, что если для какой-то переменной \(x\) выполняется, что из \(x\) достижимо \(!x\), а из \(!x\) достижимо \(x\), то задача решения не имеет. Действительно: какое бы значение для переменной \(x\) мы бы ни выбрали, мы всегда придём к противоречию — что должно быть выбрано и обратное ему значение.
Оказывается, что это условие является не только достаточным, но и необходимым. Доказательством этого факта служит описанный ниже алгоритм.
Переформулируем данный критерий в терминах теории графов. Если из одной вершины достижима вторая и наоборот, то эти две вершины находятся в одной компоненте сильной связности. Тогда критерий существования решения звучит так: для того, чтобы задача 2-SAT имела решение, необходимо и достаточно, чтобы для любой переменной \(x\) вершины \(x\) и \(!x\) находились в разных компонентах сильной связности графа импликаций.
Пусть решение существует, и нам надо его найти. Заметим, что, несмотря на то, что решение существует, для некоторых переменных может выполняться, что из \(x\) достижимо \(!x\) или из \(!x\) достижимо \(x\) (но не одновременно). В таком случае выбор одного из значений переменной \(x\) будет приводить к противоречию, в то время как выбор другого — не будет. Научимся выбирать из двух значений то, которое не приводит к возникновению противоречий. Сразу заметим, что, выбрав какое-либо значение, мы должны запустить из него обход в глубину/ширину и пометить все значения, которые следуют из него, т.е. достижимы в графе импликаций. Соответственно, для уже помеченных вершин никакого выбора между \(x\) и \(!x\) делать не нужно, для них значение уже выбрано и зафиксировано. Нижеописанное правило применяется только к непомеченным ещё вершинам.
Утверждается следующее. Пусть \(\space{\rm comp}[V]\) обозначает номер компоненты сильной связности, которой принадлежит вершина \(V\), причём номера упорядочены в порядке топологической сортировки компонент сильной связности в графе компонентов (т.е. более ранним в порядке топологической сортировки соответствуют большие номера: если есть путь из \(v\) в \(w\), то \(\space{\rm comp}[v] \leq \space{\rm comp}[w]\)). Тогда, если \(\space{\rm comp}[x] < \space{\rm comp}[!x]\), то выбираем значение !x, иначе выбираем x.
Докажем, что при таком выборе значений мы не придём к противоречию. Пусть, для определённости, выбрана вершина \(x\) (случай, когда выбрана вершина \(!x\), доказывается также).
Во-первых, докажем, что из \(x\) не достижимо \(!x\). Действительно, так как номер компоненты сильной связности \(\space{\rm comp}[x]\) больше номера компоненты \(\space{\rm comp}[!x]\) , то это означает, что компонента связности, содержащая \(x\), расположена левее компоненты связности, содержащей \(!x\), и из первой никак не может быть достижима последняя.
Во-вторых, докажем, что из любой вершины \(y\), достижимой из \(x\) недостижима \(!y\). Докажем это от противного. Пусть из \(x\) достижимо \(y\), а из \(y\) достижимо \(!y\). Так как из \(x\) достижимо \(y\), то, по свойству графа импликаций, из \(!y\) будет достижимо \(!x\). Но, по предположению, из \(y\) достижимо \(!y\). Тогда мы получаем, что из \(x\) достижимо \(!x\), что противоречит условию, что и требовалось доказать.
Итак, мы построили алгоритм, который находит искомые значения переменных в предположении, что для любой переменной \(x\) вершины \(x\) и \(!x\) находятся в разных компонентах сильной связности. Выше показали корректность этого алгоритма. Следовательно, мы одновременно доказали указанный выше критерий существования решения.
Определение. Эйлеров путь — это путь в графе, проходящий через все его рёбра.
Определение. Эйлеров цикл — это эйлеров путь, являющийся циклом.
Для простоты в обоих случаях будем считать, что граф неориентированный.
Также существует понятие гамильтонова пути и цикла — они посещают все вершины по разу, а не рёбра. Нахождение гамильтонова цикла (задача коммивояжера, англ. travelling salesman problem) — одна из самых известных NP-полных задач, в то время как нахождение эйлерового цика решается за линейное время — и мы сейчас покажем, как.
Теорема. Эйлеров цикл существует тогда и только тогда, когда степени всех вершин чётны.
Доказательство. Необходимость показывается так: можно просто взять эйлеров цикл и ориентировать все его ребра в порядке обхода. Тогда из каждой вершины будет выходить столько же рёбер, сколько входить, а значит степень у всех вершин исходного неориентированного графа была четной.
Достаточность докажем конструктивно — предъявим алгоритм нахождения.
const int maxn = 1e5;
set<int> g[maxn];
void euler(int v) {
while (!g[v].empty()) {
u = *g[v].begin();
g[v].erase(g[v].begin());
dfs(u);
}
cout << v << " ";
}Если условие на четность степеней вершин выполняется, то этот алгоритм действительно выводит эйлеров цикл, то есть последовательность из \((m+1)\) вершин, между соседними есть связи.
Следствие. Эйлеров путь существует тогда и только тогда, когда количество вершин с нечётными степенями не превосходит 2.
Кстати, аналогичная теорема есть и для ориентированного графа (можете сами попытаться сформулировать).
Доказать это можно например через лемму о рукопожатиях.
Как теперь мы будем решать задачу нахождения цикла в предположении, что он точно есть. Давайте запустимся из произвольной вершины, пройдем по любому ребру и удалим его.
void euler(int v){
stack >s;
s.push({v, -1});
while (!s.empty()) {
v = s.top().first;
int x = s.top().second;
for (int i = 0; i < g[v].size(); i++){
pair e = g[v][i];
if(!u[e.second]){
u[e.second]=1;
s.push(e);
break;
}
}
if (v == s.top().first) {
if (~x) {
p.push_back(x);
}
s.pop();
}
}
}Упражнение. Сформулируйте и докажите аналогичные утверждения для случая ориентированного графа.