Рассмотрим такую распространённую операцию как умножение двух целых чисел. Квадратичный алгоритм — умножения в столбик — все знают со школы. Долгое время предполагалось, что ничего быстрее придумать нельзя.
Первым эту гипотезу опроверг Анатолий Карацуба. Его алгоритм сводит умножение двух \(n\)-значных чисел к трём умножениям \(\frac{n}{2}\)-значных чисел, что даёт оценку времени работы
\[ T(n)=3T\left(\dfrac n 2\right)+O(n)=O\left(n^{\log_2 3}\right)\approx O(n^{1.58}) \]
Чтобы перейти к алгоритму с лучшей оценкой, нам нужно сначала установить несколько фактов о многочленах.
Обратим внимание на то, что любое число можно представить многочленом:
\[ \begin{aligned} A(x) &= a_0 + a_1\cdot x + a_2 \cdot x^2 + \dots + a_n \cdot x^n \\ &= a_0 + a_1\cdot 2 + a_2 \cdot 2^2 + \dots + a_n \cdot 2^n \end{aligned} \]
Основание x при этом может быть выбрано произвольно.
Чтобы перемножить два числа, мы можем перемножить соответствующие им многочлены, а затем произвести каррирование: пройтись от нижних разрядов получившегося многочлена и «сдвинуть» переполнившиеся разряды:
const int base = 10;
vector<int> normalize(vector<int> a) {
int carry = 0;
for (int &x : a) {
x += carry;
carry = x / base;
x %= base;
}
while (carry > 0) {
a.push_back(carry % base);
carry /= base;
}
return a;
}
vector<int> multiply(vector<int> a, vector<int> b) {
return normalize(poly_multiply(a, b));
}Прямая формула для произведения многочленов имеет вид
\[ \left(\sum_{i=0}^n a_i x^i\right)\cdot\left(\sum_{j=0}^m b_j x^j\right)=\sum_{k=0}^{n+m}x^k\sum_{i+j=k}a_i b_j \]
Её подсчёт требует \(O(n^2)\) операций, что нас не устраивает. Подойдём к этой задаче с другой стороны.
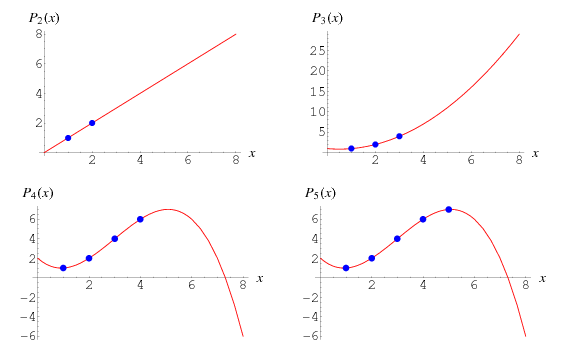
Теорема. Пусть есть набор различных точек \(x_0, x_1, \dots, x_{n}\). Многочлен степени \(n\) однозначно задаётся своими значениями в этих точках. (Коэффициентов у этого многочлена столько же, сколько и точек — прим. К. О.)
Доказательство будет конструктивным — можно явным образом задать многочлен, который принимает заданные значения \(y_0, y_1, \ldots, y_n\) в этих точках:
\[ y(x)=\sum\limits_{i=0}^{n}y_i\prod\limits_{j\neq i}\dfrac{x-x_j}{x_i-x_j} \]
Корректность. Проверим, что в точке \(x_i\) значение действительно будет равно \(y\):
Для \(i\)-го слагаемого внутреннее произведение будет равно единице, если вместо \(x\) подставить \(x_i\): в этом случае просто перемножается \((n-1)\) единица. Эта единица помножится на \(y_i\) и войдёт в сумму.
Для всех остальных слагаемых произведение занулится: один из множетелей будет равен \((x_i - x_i)\).
Уникальность. Предположим, есть два подходящих многочлена степени \(n\) — \(A(x)\) и \(B(x)\). Рассмотрим их разность. В точках \(x_i\) значение получившегося многочлена \(A(x) - B(x)\) будет равняться нулю. Если так, то точки \(x_i\) должны являться его корнями, и тогда разность можно записать так:
\[ A(x) - B(x) = \alpha \prod_{i=0}^n (x-x_i) \]
для какого-то числа \(\alpha\). Тут мы получаем противоречие: если раскрыть это произведение, то получится многочлен степени \(n+1\), который нельзя получить разностью двух многочленов степени \(n\).
Этот многочлен называется интерполяционным многочленом Лагранжа, а сама задача проведения многочлена через точки — интерполяцией.
Примечание. На практике интерполяцию решают методом Гаусса: её можно свести к решению линейного уравнения \(aX = y\), где \(X\) это матрица следующего вида:
\[ \begin{pmatrix} 1 & x_0 & x_0^2 & \ldots & x_0^n \\ 1 & x_1 & x_1^2 & \ldots & x_1^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \ldots & x_n^n \\ \end{pmatrix} \]
Важный факт: многочлен можно однозначно задать не только своими коэффициентами, но также корнями и значениями хотя бы в \((n+1)\)-ой точке.
Что происходит со значениями многочлена-произведения \(A(x) B(x)\) в конкретной точке \(x_i\)? Оно просто становится равным \(A(x_i) B(x_i)\).
Основная идея алгоритма: если мы знаем значения в каких-то различных \(n + m\) точках для обоих многочленов \(A\) и \(B\), то, попарно перемножив их, мы за \(O(n + m)\) операций можем получить значения в тех же точках для многочлена \(A(x) B(x)\) — а с их помощью можно интерполяцией получить исходный многочлен и решить задачу.
vector<int> poly_multiply(vector<int> a, vector<int> b) {
vector<int> A = evaluate(a);
vector<int> B = evaluate(b);
for (int i = 0; i < A.size(); i++)
A[i] *= B[i];
return interpolate(A);
}Если притвориться, что evaluate и interpolate работают за линейное время, то умножение тоже будет работать за линейное время.
К сожалению, непосредственное вычисление значений требует \(O(n^2)\) операций, а интерполяция — как методом Гаусса, так и через символьное вычисление многочлена Лагранжа — и того больше, \(O(n^3)\).
Но что, если бы мы могли вычислять значения в точках и делать интерполяцию быстрее?
Определение. Комплексные числа — это числа вида \(a + bi\), где \(a\) и \(b\) это обычные вещественные числа, а \(i\) это так называемая мнимая единица: это число, для которого выполняется равенство \(i^2 = -1\).
Комплексные числа ввели в алгебре, чтобы работать с корнями из отрицательных чисел: \(i\) в каком-то смысле равно \(\sqrt{-1}\). Так же, как и отрицательные числа, они как бы «не существуют» в реальном мире, а только в сознании математиков.
С комплексными числами можно работать почти так же, как с действительными. Они даже удобнее: все квадратные корни всегда извлекаются, все корни многочленов всегда находятся.
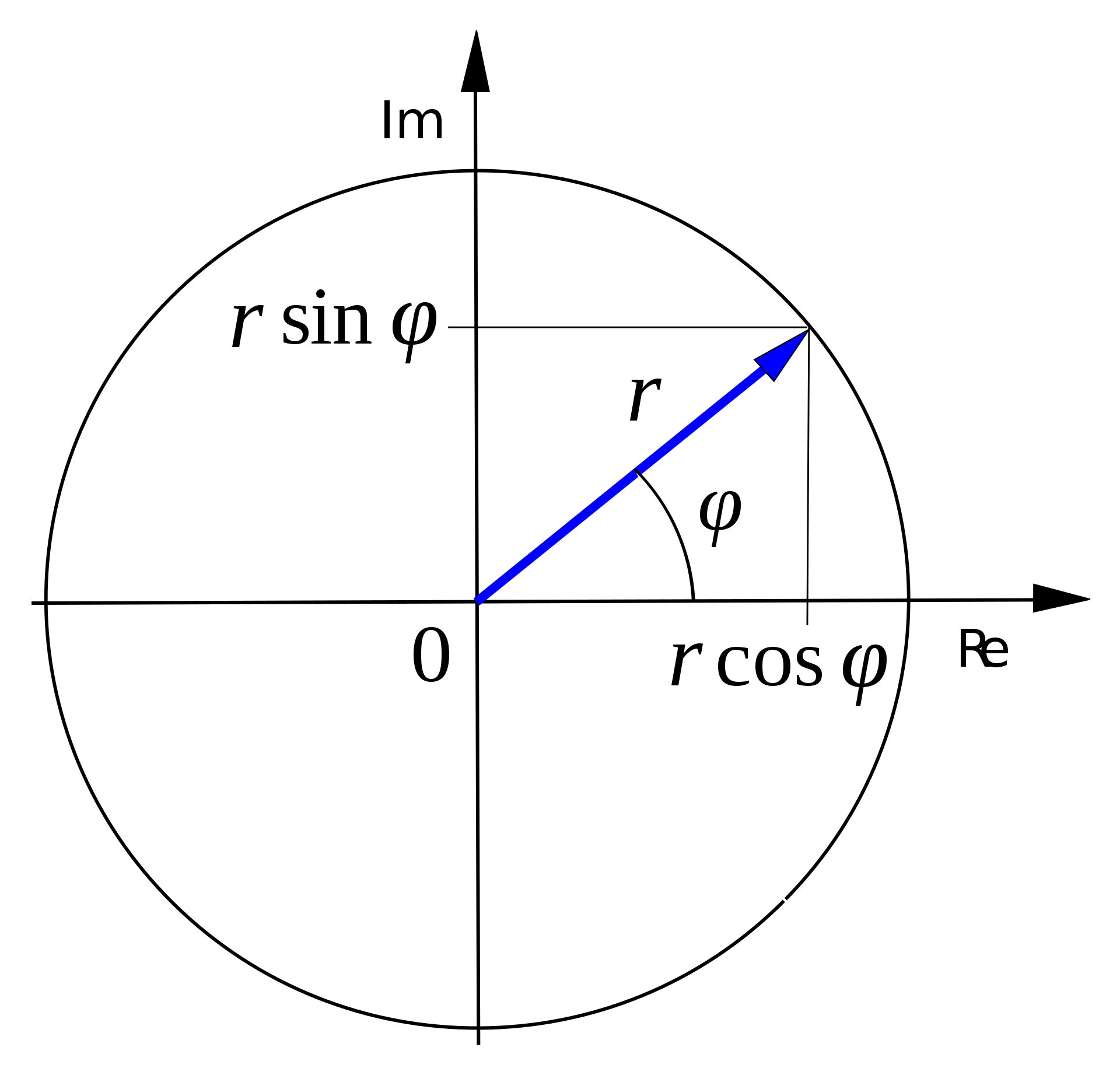
Комплексные числа удобно изображать на плоскости в виде вектора \((a, b)\) и считать через них всякую геометрию.
Модулем комплексного числа называется действительное число \(r = \sqrt{a^2 + b^2}\) . Геометрически, это длина вектора \((a, b)\).
Аргументом комплексного числа называется действительное число \(\phi \in (-\pi, \pi]\), для которого выполнено \(\tan \phi = \frac{b}{a}\). Геометрически, это значение угла между \((a, 0)\) и \((a, b)\). Для нуля — вектора \((0, 0)\) — аргумент не определён.
Таким образом комплексное число можно представить в полярных координатах:
\[ a+bi = r ( \cos \phi + i \sin \phi ) \]
Подобное представление удобно по следующей причине: чтобы перемножить два комплексных числа, нужно перемножить их модули и сложить аргументы.
Упражнение. Докажите это.
Определим число Эйлера \(e\) как число со следующим свойством:
\[ e^{i\phi} = \cos \phi + i \sin \phi \]
Просто введём такую нотацию для выражения \(\cos \phi + i \sin \phi\). Не надо думать, почему это так.
Геометрически, все такие точки живут на единичном круге:
Такая нотация удобна, потому что можно обращаться с \(e^{i\phi}\) как с обычной экспонентой. Пусть мы, например, хотим перемножить два числа на единичном круге с аргументами \(a\) и \(b\). Тогда это можно записать так:
\[ (\cos a + i \sin a) \cdot (\cos b + i \sin b) = e^{i (a+b)} \]
Упражнение. Проверьте это: раскройте скобки и проделайте немного алгебры.
У комплексных чисел есть много других замечательных свойств, но нам для алгоритма на самом деле потребуется только следующее:
Утверждение. Для любого натурального \(n\) есть ровно \(n\) комплексных «корней из единицы», то есть чисел \(w_k\), для которых выполнено:
\[ w_k^n = 1 \]
А именно, это будут числа вида:
\[ w_k = e^{i \tau \frac{k}{n}} \]
где \(\tau\) обозначает \(2 \pi\), «целый круг». Это довольно новая нотация.
На комплексной плоскости эти числа располагаются на единичном круге на равном расстоянии друг от друга:
Первый корень \(w_1\) (точнее второй — единицу считаем нулевым корнем) называют образующим корнем степени \(n\) из единицы. Возведение его в нулевую, первую, вторую и так далее степени порождает последовательность нужных корней единицы, при этом на \(n\)-ном элементе последовательность зацикливается:
\[ w_n = e^{i \tau \frac{n}{n}} = e^{i \tau} = e^{i \cdot 0} = w_0 = 1 \]
Будем обозначать \(w_1\) как просто \(w\).
Упражнение. Докажите, что других корней быть не может.
Дискретным преобразованием Фурье называется вычисление значений многочлена в комплексных корнях из единицы:
\[ y_j = \sum_{k=0}^{n-1} x_n e^{i\tau \frac{kj}{n}} = \sum_{k=0}^{n-1} x_n w_1^{kj} \]
Обратным дискретным преобразованием Фурье называется, как можно догадаться, обратная операция — интерполяция коэффициентов \(x_i\) по значениям \(X_i\).
\[ x_j = \frac{1}{n} \sum_{k=0}^{n-1} y_n e^{-i\tau \frac{kj}{n}} = \frac{1}{n} \sum_{k=0}^{n-1} y_n w_{n-1}^{kj} \]
Почему эта формула верна? При вычислении ПФ мы практически применяем матрицу к вектору:
\[ \begin{pmatrix} w^0 & w^0 & w^0 & w^0 & \dots & w^0 \\ w^0 & w^1 & w^2 & w^3 & \dots & w^{-1} \\ w^0 & w^2 & w^4 & w^6 & \dots & w^{-2} \\ w^0 & w^3 & w^6 & w^9 & \dots & w^{-3} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ w^0 & w^{-1} & w^{-2} & w^{-3} & \dots & w^1 \end{pmatrix}\begin{pmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n-1} \end{pmatrix} = \begin{pmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1} \end{pmatrix} \]
То есть преобразование Фурье — это просто линейная операция над вектором: \(W a = y\). Значит, обратное преобразование можно записать так: \(a = W^{-1}y\).
Как будет выглядеть эта \(W^{-1}\)? Автор не будет пытаться изображать логичный способ рассуждений о её получении и сразу её приведёт:
\[ W^{-1} = \dfrac 1 n\begin{pmatrix} w^0 & w^0 & w^0 & w^0 & \dots & w^0 \\ w^0 & w^{-1} & w^{-2} & w^{-3} & \dots & w^{1} \\ w^0 & w^{-2} & w^{-4} & w^{-6} & \dots & w^{2} \\ w^0 & w^{-3} & w^{-6} & w^{-9} & \dots & w^{3} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ w^0 & w^{1} & w^{2} & w^{3} & \dots & w^{-1} \end{pmatrix} \]
Проверим, что при перемножении \(W\) и \(W^{-1}\) действительно получается единичная матрица:
Значение \(i\)-того диагонального элемента будет равно \(\frac{1}{n} \sum_k w^{ki} w^{-ki} = \frac{1}{n} n = 1\).
Значение любого недиагонального (\(i \neq j\)) элемента \((i, j)\) будет равно \(\frac{1}{n} \sum_k w^{ik} w^{-jk} = \frac{1}{n} \sum_k w^k w^{i-j} = \frac{w^{i-j}}{n} \sum_k w^k = 0\), потому что все комплексные корни суммируются в ноль, то есть \(\sum w^k = 0\) (см. картинку — там всё симметрично).
Внимательный читатель заметит симметричность форм \(W\) и \(W^{-1}\), а также формул для прямого и обратного преобразования. На самом деле, эта симметрия нам сильно упростит жизнь: для обратного преобразования Фурье можно использовать тот же алгоритм, только вместо \(w^k\) использовать \(w^{-k}\), а в конце результат поделить на \(n\).
Напомним, что мы изначально хотели перемножать многочлены следующим алгоритмом:
Посчитаем значения в \(n+m\) каких-нибудь точках обоих многочленов
Перемножим эти значения за \(O(n+m)\).
Интерполяцией получим многочлен-произведение.
В общем случае быстро посчитать интерполяцию и даже просто посчитать значения в точках нельзя, но для корней единицы — можно. Если научиться быстро считать значения в корнях и интерполировать (прямое и обратное преобразование Фурье), но мы можно решить исходную задачу.
Соответствующий алгоритм называется быстрым преобразованием Фурье (англ. fast Fourier transform). Он использует парадигму «разделяй-и-властвуй» и работает за \(O(n \log n)\).
Обычно, алгоритмы «разделяй-и-властвуй» делят задачу на две половины: на первые \(\frac{n}{2}\) элементов и вторые \(\frac{n}{2}\) элементов. Здесь мы поступим по-другому: поделим все элементы на чётные и нечётные.
Представим многочлен в виде \(P(x)=A(x^2)+xB(x^2)\), где \(A(x)\) состоит из коэффициентов при чётных степенях \(x\), а \(B(x)\) — из коэффициентов при нечётных.
Пусть \(n = 2k\). Тогда заметим, что
\[ w^{2t}=w^{2t \bmod 2k}=w^{2(t \bmod k)} \]
Зная это, исходную формулу для значения многочлена в точке \(w^t\) можно записать так:
\[ P(w^t) = A(w^{2t}) + w^t B(w^{2t}) = A\left(w^{2(t\bmod k)}\right)+w^tB\left(w^{2(t\bmod k)}\right) \]
Ключевое замечание: корней вида \(w^{2t}\) в два раза меньше, потому что \(w^n = w^0\), и можно сказать, что.
У нас по сути в два раза меньше корней (но они так же равномерно распределены на единичной окружности) и в два раза меньше коэффициентов — мы только что успешно уменьшили нашу задачу в два раз.
Сам алгоритм заключается в следующем: рекурсивно посчитаем БПФ для многочленов \(A\) и \(B\) и объединим ответы с помощью формулы выше. При этом в рекурсии нам нужно считать значения на корнях степени не \(n\), а \(k = \frac{n}{2}\), то есть на всех «чётных» корнях степени \(n\) (вида \(w^{2t}\)).
Заметим, что если \(w\) это образующий корень степени \(n = 2k\) из единицы, то \(w^2\) будет образующим корнем степени \(k\), то есть в рекурсию мы можем просто передать другое значение образующего корня.
Таким образом, мы свели преобразование размера \(n\) к двум преобразованиям размера \(\dfrac n 2\). Следовательно, общее время вычислений составит
\[ T(n)=2T\left(\dfrac n 2\right)+O(n)=O(n\log n) \]
Заметим, что предположение о делимости \(n\) на \(2\) имело существенную роль. Значит, \(n\) должно быть чётным на каждом уровне, кроме последнего, из чего следует, что \(n\) должно быть степенью двойки.
Приведём код, вычисляющий БПФ по схеме Кули-Тьюки:
typedef complex<double> ftype;
const double pi = acos(-1);
template<typename T>
vector<ftype> fft(vector<T> p, ftype w) {
int n = p.size();
if(n == 1)else { {
return {p[0]};
else {
vector<T> AB[2];
for(int i = 0; i < n; i++)
AB[i % 2].push_back(p[i]);
auto A = fft(AB[0], w * w);
auto B = fft(AB[1], w * w);
vector<ftype> res(n);
ftype wt = 1;
int k = n / 2;
for(int i = 0; i < n; i++) {
res[i] = A[i % k] + wt * B[i % k];
wt *= w;
}
return res;
}
}
vector<ftype> evaluate(vector<int> p) {
while(__builtin_popcount(p.size()) != 1)
p.push_back(0);
return fft(p, polar(1., 2 * pi / p.size()));
}Как обсуждалось выше, обратное преобразование Фурье удобно выразить через прямое:
vector<int> interpolate(vector<ftype> p) {
int n = p.size();
auto inv = fft(p, polar(1., -2 * pi / n));
vector<int> res(n);
for(int i = 0; i < n; i++)
res[i] = round(real(inv[i]) / n);
return res;
}Теперь мы умеем перемножать два многочлена за \(O(n \log n)\):
vector<int> poly_multiply(vector<int> a, vector<int> b) {
vector<int> A = fft(a);
vector<int> B = fft(b);
for (int i = 0; i < A.size(); i++)
A[i] *= B[i];
return interpolate(A);
}Примечание. Приведённый выше код, являясь корректным и имея асимптотику \(O(n\log n)\), едва ли пригоден для использования на реальных контестах. Он имеет большую константу и далеко не так численно устойчивый, чем оптимальные варианты написания быстрого преобразования Фурье. Мы его приводим, потому что он относительно простой.
Читателю рекомендуется самостоятельно задуматься о том, как можно улучшить время работы и точность вычислений. Из наиболее важных недостатков:
внутри преобразования не должно происходить выделений памяти
работать желательно с указателями, а не векторами
корни из единицы должны быть посчитаны наперёд
Следует избавиться от операций взятия остатка по модулю
Вместо вычисления преобразования с \(w^{-1}\) можно вычислить преобразование с \(w\), а затем развернуть элементы массива со второго по последний.
Здесь приведена одна из условно пригодных реализаций.
Но главная проблема в численной стабильности — мы нарушили первое правило действительных чисел. Однако, от неё можно избавиться.
Нам от комплексных чисел на самом деле нужно было только одно свойство: что у единицы есть \(n\) «корней». На самом деле, помимо комплексных чисел, есть и другие алгебраические объекты, обладающие таким свойством — например, элементы кольца вычетов по модулю.
Нам нужно просто найти такую пару \(m\) и \(g\) (играющее роль \(w_n^1\)), такую что \(g\) является образующим элементом, то есть \(g^n \equiv 1 \pmod m\) и при для всех остальных \(k < n\) все степени \(g^k\) различны по модулю \(m\). В качестве \(m\) на практике часто специально берут «удобные» модули, например
\[ m = 998244353 = 7 \cdot 17 \cdot 2^{23} + 1 \]
Это число простое, и при этом является ровно на единицу больше числа, делящегося на большую степень двойки. При \(n=2^23\) подходящим \(g\) является число \(31\). Заметим, что, как и для комплексных чисел, если для некоторого \(n=2^k\) первообразный корень - \(g\), то для \(n=2^{k-1}\) первообразным корнем будет \(g^2 (mod m)\). Таким образом, для \(m=998244353\) и \(n=2^k\) первообразный корень будет равен \(g=31 \cdot 2^{23-k} (mod m)\).
Реализация практически не отличается.
const int MOD = 998244353, W = 805775211, IW = 46809892;
const int MAXN = (1 << 19), INV2 = 499122177;
// W - первообразный корень MAXN-ной степени из 1, IW - обратное по модулю MOD к W
// Первообразный корень (1 << 23)-й степени из 1 по модулю MOD равен 31; тогда первообразный корень (1 << X)-й степени для X от 1 до 23 равен (31 * (1 << (23 - X))) % MOD
// INV2 - обратное к двум по модулю MOD
// Данная реализация FFT перемножает два целых числа длиной до 250000 цифр за ~0.13 секунд без проблем с точностью и занимает всего 30 строк кода
int pws[MAXN + 1], ipws[MAXN + 1];
void init() {
pws[MAXN] = W; ipws[MAXN] = IW;
for (int i = MAXN / 2; i >= 1; i /= 2) {
pws[i] = (pws[i * 2] * 1ll * pws[i * 2]) % MOD;
ipws[i] = (ipws[i * 2] * 1ll * ipws[i * 2]) % MOD;
}
}
void fft(vector<int> &a, vector<int> &ans, int l, int cl, int step, int n, bool inv) {
if (n == 1) { ans[l] = a[cl]; return; }
fft(a, ans, l, cl, step * 2, n / 2, inv);
fft(a, ans, l + n / 2, cl + step, step * 2, n / 2, inv);
int cw = 1, gw = (inv ? ipws[n] : pws[n]);
for (int i = l; i < l + n / 2; i++) {
int u = ans[i], v = (cw * 1ll * ans[i + n / 2]) % MOD;
ans[i] = (u + v) % MOD;
ans[i + n / 2] = (u - v) % MOD;
if (ans[i + n / 2] < 0) ans[i + n / 2] += MOD;
if (inv) {
ans[i] = (ans[i] * 1ll * INV2) % MOD;
ans[i + n / 2] = (ans[i + n / 2] * 1ll * INV2) % MOD;
}
cw = (cw * 1ll * gw) % MOD;
}
}С недавнего времени некоторые проблемсеттеры начали использовать именно этот модулю вместо стандартного \(10^9+7\), чтобы намекнуть (или сбить с толку), что задача на FFT.
Даны две бинарные строки \(a\) и \(b\). Нужно найти такой циклический сдвиг строки \(b\), что количество совпадающих соответствующих символов с \(a\) станет максимально.
Сперва научимся для каждого циклического сдвига \(i\) второй строки считать количество совпадающих единиц \(c_i\). Это можно сделать за \(O(n^2)\) множеством разных способов, мы рассмотрим следующий: рассмотрим каждую единицу во втором числе, пусть она стоит на \(j\)-й позиции; для каждого \(l\) от \(0\) до \(n-1\), если \(a_l\) равно 1, то прибавим один к \(c_{i-j}\) (при этом \(i-j\) берётся по модулю \(n\)). Такой алгоритм верный, потому что по сути мы перебираем пары единиц, которые могут совпадать, и прибавляем +1 к количеству совпадающих единиц для соответствующего циклического сдвига. И тут мы можем заметить очень важную вещь: если перемножить числа, соответствующие \(a\) и \(b\), в столбик и не переносить разряды при сложении, то мы получим как раз массив \(c\) (с одним нюансом: его длина может быть больше \(n\), тогда нам нужно для всех \(i \geq n\) прибавить \(c_i\) к \(c_{i-n}\))! А перемножать длинные числа мы уже научились: это легко сделать при помощи БПФ. Таким образом, мы научились искать число совпадающих единиц; заметим, что мы можем инвертировать биты в строках и применить эквивалентный алгоритм, получив в итоге количества совпадающих нулей. Сложим соответствующие элементы в двух массивах и найдём индекс максимального. Также очень часто в задачах на FFT требуется не явно перемножить два полинома, а посчитать свёртку двух векторов. Прямой свёрткой векторов \(a\) длины \(n\) и \(b\) длины \(m\) называется вектор \(s\) длины \(n+m-1\) такой, что \(s_k = \Sigma_{i=0}^{k} a_i \cdot b_{k-i} (\forall k \in [0;n+m-2])\) (при этом считается, что несуществующие элементы равны нулю). Круговой (циклической) свёрткой векторов \(a\) и \(b\) длины \(n\) называется вектор \(s\) длины \(n\) такой, что \(s_k = \Sigma_{i=0}^{n-1} a_i \cdot b_{k-i} (\forall k \in [0; n-1])\) (при этом \({k-i}\) берётся по модулю \(n\)). Оказывается, что линейную свёртку можно считать через круговую: для этого дополним нулями оба вектора до одинаковой длины \(n+m-1\). Это очень легко доказать: если для некоторого \(k\) \(i \geq k+1\), то либо \(a_i\), либо \(b_{k-i}\) будут равны нулю. Если расписать выражение для прямого преобразования Фурье круговой свёртки и перенести множетили, то можно получить, что круговая свёртка равна вектору произведений многочленов с коэффициентами \(a\) и \(b\) в точках \(0,1,\dots n-1\). Возможно, когда-нибудь я это распишу.