Дерево называется корневым, если оно ориентированно, и из какой-то вершины (называемой корнем) можно попасть во все остальные.
Примеры корневых деревьев:
Задачи на корневые деревья весьма бесполезны в реальной жизни, но зато очень интересны с алгоритмической точки зрения, и поэтому часто встречаются на олимпиадах по программированию.
Посчитаем для каждой вершины времена входа (\(tin\)) и выхода (\(tout\)) из неё во время эйлерова прохода:
vector<int> g[maxn];
int p[maxn], tin[maxn], tout[maxn];
int t = 0;
void dfs (int v) {
tin[v] = t++;
for (int u : g[v])
dfs(u);
tout[v] = t; // иногда счётчик тут тоже увеличивают
}У этих массивов много полезных свойств:
Последнее свойство на самом деле очень важное. Его можно использовать для обработки разных запросов на поддеревьях, сводя их к запросам на подотрезках, которые уже можно решать стандартными методами — например, через дерево отрезков.
Пример задачи:
Есть корневое дерево. Рядом с каждой вершиной записано число. Поступают два типа запросов: прибавить ко всем вершинам на каком-то поддереве число \(x_i\) и найти значение числа у вершины \(v_i\).
Выпишем все числа у вершин в один массив, в позиции, соответствующие их \(tin\)-ам. Что такое «прибавить на поддереве» относительно этого массива? Это то же, самое, что прибавить какую-то константу на каком-то подотрезке, а это можно делать любой достаточно продвинутой структурой.
Дано корневое дерево. Требуется отвечать на запросы нахождения \(d_i\)-того предка вершины \(v_i\), то есть вершины-предка, находящейся на расстоянии \(d_i\) от \(v_i\).
Создадим \(h\) векторов, где \(h\) — высота дерева. Для каждой вершины, во время прохода в dfs, добавим её \(tin\) в вектор, соответствующей её глубине. Получаем \(h\) отсортированных векторов.
Теперь заметим, что внутри одного вектора все отрезки поддеревьев вершин — \([tin_v, tout_v)\) — тоже не пересекаются, а значит ещё и отсортированы. Тогда ответа на запрос мы можем просто взять \(tin\) вершины-запроса, посмотреть на вектор нужного уровня и за \(O(\log n)\) сделать бинпоиск по нужному отрезку.
Также существует другой способ, требующий \(O(1)\) времени на запрос, но \(O(n \log n)\) памяти на предпосчёт — лестничная декомпозиция.
Для большого класса задач требуется решить следующую вспомогательную:
Дано корневое дерево. Требуется отвечать на запросы нахождения наименьшего общего предка вершин \(u_i\) и \(v_i\), то есть вершины \(w\), которая лежит на пути от корня до \(u_i\), на пути от корня до \(v_i\), и при этом самую глубокую (нижнюю) из всех таких.
По-английский эта задача называется Least Common Ancestor. Есть много разных способов её решать, и мы рассмотрим только основные.
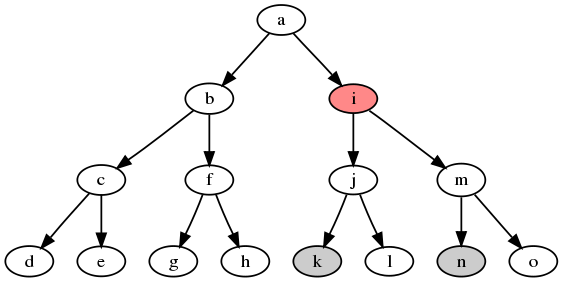
Для лучшего понимания — медленно (за линейное время) наименьшего общего предка можно искать так:
bool a (int u, int v) {
return tin[u] <= tin[v] && tin[v] < tout[u];
}
int lca (int u, int v) {
while (!ancestor(u, v))
u = p[u];
return u;
}Предпосчитаем для каждой вершины её 1-го предка, 2-го предка, 4-го и так далее. Сохраним их в двумерном массиве up размера \(n \times \lceil \log n \rceil\): в up[v][d] будет храниться предок вершины \(v\) на расстоянии \(2^d\), а если такой вершины не существует, то корень.
Такой препроцессинг можно выполнить за \(O(n \log n)\), используя тот факт, что предок на расстоянии \(2^{d+1}\) — это предок на расстоянии \(2^d\) предка на расстоянии \(2^d\):
int up[maxn][logn];
void dfs (int v) {
for (int l = 1; l < logn; l++)
up[v][l] = up[up[v][l-1]][l-1];
tin[v] = t++;
for (int u : g[v]) {
up[u][0] = v;
dfs(u);
}
tout[v] = t;
}Пусть теперь поступил запрос нахождения LCA — пара вершин \((u, v)\):
up, будем подниматься по предкам одной из них, пока не найдём самую высокую вершину, которая ещё не является предком другой. Следующая за ней будет искомым LCA.Подробнее про второй пункт. Присвоим \(i = \lceil \log n \rceil\) и будем уменьшать эту переменную на единицу, пока up[v][i] не перестанет быть предком \(u\). Когда это произойдёт, подвинем указатель на \(2^i\)-го предка \(v\) и продолжим дальше:
int lca (int v, int u) {
if (a(v, u)) return v;
if (a(u, v)) return u;
for (int l = logn-1; l >= 0; l--)
if (!ancestor(up[v][l], u))
v = up[v][l];
return up[v][0];
}Указатель up[v][i] изначально явдяеься корнем дерева, а затем будет каждую итерацию спускаться на \(2^i\). Когда он станет потомком lca, нам достаточно подняться всего лишь один раз, потому что два раза прыгнуть на расстояние \(2^i\) это то же самое, что один раз прыгнуть на \(2^{i+1}\), а мы могли это сделать на предыдущем шаге.
Асимптотика. Препроцессинг занимает \(O(n \log n)\), потому что таков размер массива up, и каждый его элемент вычисляется за константу. Ответ на произвольный запрос будет работать за \(O(\log n)\), потому что фактически мы делаем один бинпоиск.
Пусть нас вместо LCA спрашивают, например, о минимуме на произвольном пути (на всех рёбрах записаны какие-то числа).
Мы можем сделать такой же предподсчет, как в методе двоичных подъемов, но хранить вместе с номером \(2^d\)-ого предка минимум на соответствующем пути.
Заметим, что минимум на пути от \(u\) до \(v\) — это минимум от минимума на пути от \(u\) до \(lca(u, v)\) и от минимума на пути от \(v\) до \(lca(u, v)\). В свою очередь, оба этих минимума — это минимум на всех двоичных подъемах до LCA.
int get_min (int v, int u) {
int res = inf;
for (int l = logn-1; l >= 0; l--)
if (!ancestor(up[v][l], u))
v = up[v][l], res = min(res, mn[v][l]);
for (int l = logn-1; l >= 0; l--)
if (!ancestor(up[u][l], v))
u = up[u][l], res = min(res, mn[u][l]);
return min({res, mn[v][0], mn[u][0]})
}Аналогичным образом можно считать сумму, gcd, полиномиальный хэш и много других странных функций на пути, но только в статическом случае (когда у нас нет обновлений). Для динамического случая существует весьма сложный метод, называемый heavy-light декомпозицией.
Подойдём к задаче нахождения наименьшего общего предка с другой стороны.
Пройдёмся по дереву dfs-ом и выпишем два массива: глубины вершин и номера вершин. Записывать мы их будем как когда при входе в вершину, так и при выходе.
Пусть теперь поступил запрос: найти LCA вершин \(v\) и \(u\). Для определенности предположим, что \(tin_v < tin_u\), то есть \(v\) в обходе встретилась раньше. Посмотрим на часть выписанного пути между моментом, когда мы вышли из \(v\) и моментом, когда мы в первый раз вошли в \(u\). Где-то на этом отрезке мы должны были прийти в наименьший общий предок, так как любой простой путь между двумя вершинами в дереве единственный. При этом мы на этом пути не поднимались куда-то выше LCA, а значит LCA — это самая высокая вершина на этом пути.
Получается, что чтобы найти LCA, можно найти позицию минимума на отрезке \([tout_v, tin_u]\) в массиве глубин (первый выписанный массив) и посмотреть, какой вершине она соответствует в эйлеровом обходе (второй выписанный массив). Таким образом, задачу LCA можно свести к задаче RMQ (нахождению минимума на отрезке), что можно сделать тем же деревом отрезков.
На практике асимптотику мы особо не улучшили — пока что всё равно требуется \(O(\log n)\) времени на запрос в дерево отрезков, хоть преподсчёт и будет уже линейным.
Асимптотику времени запроса можно улучшить, используя тот факт, что мы на самом деле решаем задачу static RMQ, то есть у нас нет изменений этого массива. Для этого есть более подходящая структура — разреженная таблица. Она позволяет отвечать на запрос минимума за \(O(1)\), но использует \(O(n \log n)\) операций на препроцессинг (с малой константой). Подробнее про неё можно почитать в отдельной статье.
Примечание: алгоритм нахождения RMQ, описываемый в этой секции, абсолютно бесполезен на практике, однако очень интересен с теоретической точки зрения.
Оказывается, что и LCA, и static RMQ можно считать за \(O(1)\) времени на запрос и \(O(n)\) времени на предпосчёт.
На самом деле, мы решаем не совсем полноценную задачу RMQ. Мы работаем не со всеми массивами целых чисел от 1 до \(n\), а только с некоторыми — с теми, в которых любые два элемента отличаются ровно на единицу, потому что каждый переход это либо спуск, либо подъём в dfs. Это ограничение позволяет находить минимум на подотрезках подобных массивов быстрее.
Сделаем следующее: раз каждые два элемента отличаются на единицу, то сопоставим исходному массиву глубин булевый массив размера \((n-1)\): на \(i\)-той позиции будет стоять единица, если следующее значение больше, и ноль в противном случае. Этот массив нужно будет хранить в бинарном виде, чтобы можно было за константу получать булеву маску небольших подотрезков.
Первая часть предподсчёта. Возьмем константу \(k = \lfloor \frac{\log n}{2} \rfloor\), и разделим исходный массив на блоки по \(k\) элементов. На каждом блоке посчитаем минимум, а над этими минимумами построим sparse table.
Всего блоков таких блоков \(O(\frac{2 n}{\log n})\), и поэтому построение работает за линейное время:
\[ O(\frac{2 n}{\log n} \log \frac{2 n}{\log n}) = O(\frac{2 n}{\log n} (\log 2n - \log \log n)) = O(n) \]
Вторая часть предподсчёта. Посчитаем для каждой возможной маски подъёмов / спусков размера \(k\) максимальный спуск на ней — то есть пройдёмся по ней, поддерживая разницу встретившихся нулей и единиц, и запомним минимальное значение этого баланса. Это можно сделать за длину маски, помоноженное на их количество:
\[ O(k \cdot 2^k) = O(\frac{\log n}{2} 2^{\frac{\log n}{2}}) = O(\sqrt n \log n) \]
Возможных масок получается немного — ради этого мы и делили логарифм на два при определении \(k\)
Запрос. Нам нужно с помощью посчитанных структур найти RMQ на каком-то отрезке \([l, r]\). Он включает в себя какие-то последовательные блоки и сколько-то оставшихся ячеек слева и справа, не вошедших ни в какой целый блок.
Для блочной части мы можем просто сделать запрос в sparse table — он будет работать за константу.
Для обеих не-блочных частей посчитаем ещё по кандидату на ответ. Для этого нужно прибавить к граничному элементу предподсчитанное значение минимума на маске оставшихся неблочных элементов — её можно за константу получить битовыми операциями над булевым массивом.
Просто посчитать все суффиксные и префиксные минимумы для всех блоков, чтобы обрабатывать второй случай, к сожалению, нельзя — есть один частный случай, когда запрос маленький и не накрывает никакой блок целиком. В данном случае нужно просто взять граничный элемент и прибавить к нему минимум от нужной маски из массива подъёмов.
Наоборот. Этот алгоритм очень важен с теоретической точки зрения, потому что позволяет решать, не только LCA, но и в общем случае static RMQ за линейное время.
Построим декартово дерево, в котором в качестве ключей \(x_i\) возьмём индексы элементов, а в качестве приоритетов \(y_i\) возьмём сами значения. Декартово дерево могло получиться несбалансированным (так как нет рандомизации приоритетов), но это нам и не нужно. Дальше просто применим описанный выше алгоритм к этому дереву, и теперь для нахождения минимума в исходном массиве можно просто запросить общего предка \(l\)-той и \(r\)-той вершины в дереве — его приоритет в декартовом дереве и будет искомым минимумом.
Чуть более подробно и с реализацией (автор это никогда не кодил и вам не советует) можно почитать у Емакса. Впрочем, на практике этот алгоритм использовать нецелесообразно из-за большой константы: слишком много чего нужно считать, чтобы избавиться от логарифма в асимптотике.