Разреженная таблица (англ. sparse table) — структура данных, позволяющая отвечать на запросы минимума на отрезке за \(O(1)\) с препроцессингом за \(O(n \log n)\) времени и памяти.
Определение. Разреженная таблица — это следующий двумерный массив размера \(\log n \times n\):
\[ t[k][i] = \min \{ a_i, a_{i+1}, \ldots, a_{i+2^k-1} \} \]
По-русски: считаем минимумы на каждом отрезке длины \(2^k\).
Такой массив можно посчитать за его размер, итерируясь либо по \(i\), либо по \(k\):
\[ t[k][i] = \min(t[k-1][i], t[k-1][i+2^{k-1}]) \]
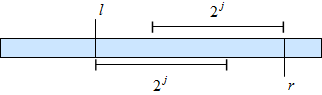
Имея таком массив, мы можем для любого отрезка быстро посчитать минимум на нём. Заметим, что у любого отрезка имеется два отрезка длины степени двойки, которые пересекаются, и, главное, покрывают его и только его целиком. Значит, мы можем просто взять минимум из значений, которые соответствуют этим отрезкам.
Последняя деталь: для того, чтобы константа на запрос стала настоящей, нужно научиться считать сам логарифм за константу. Для этого можно воспользоваться доступной в GCC функцией __lg. Она внутри использует инструкцию clz (“count leading zeros”), которая присутствует в большинстве современных процессоров и возвращает количество нулей до первой единицы в бинарной записи, из чего за несколько процессорных тактов можно получить нужный округленный логарифм.
int a[maxn], mn[logn][maxn];
int rmq(int l, int r) { // полуинтервал [l; r)
int t = __lg(r - l);
return min(mn[t][l], mn[t][r - (1 << t)]);
}
// Это считается где-то в первых строчках main:
memcpy(mn[0], a, sizeof a);
for (int l = 0; l < logn - 1; l++)
for (int i = 0; i + (2 << l) <= n; i++)
mn[l+1][i] = min(mn[l][i], mn[l][i + (1 << l)]);Для больших таблиц порядок итерирования и расположение данных в памяти сильно влияет на скорость построения — это связано с работой кэшей. Но в большинстве случаев время построения не так критично.
Упражнение. Подумайте, в чём недостатки других 4 вариантов итерирования и layout-а.
Интересно, что последний цикл не векторизуется компилятором автоматически (видимо, потому что std::min это что-то сложное внутри), и поэтому замена тела цикла на конструкцию вида (x < y ? x : y) ускоряет построение ещё в ~2 раза.
Разреженная таблица является статической структурой данных, то есть её нельзя дёшево обновлять (но можно достраивать на ходу — см. задачу «Антиматерия» с РОИ-2017).
Разреженную таблицу часто применяют для решения задачи о наименьшем общем предке, так как её можно свести к RMQ.
Эту структуру тоже можно обобщить на большие размерности. Пусть мы хотим посчитать RMQ на подквадратах. Тогда вместо массива t[k][i] у нас будет массив t[k][i][j], в котором вместо минимума на отрезах будет храниться минимум на квадратах тех же степеней двоек. Получение минимума на произвольном квадрате тогда уже распадется на четыре минимума на квадратах длины \(2^k\).
В общем же случае от нас просят минимум на прямоугольниках \(d\)-мерного массива. Тогда делаем предподсчет, аналогичный предыдущему случаю, только теперь тут будет \(O(n \log^d n)\) памяти и времени на предподсчет — нужно хранить минимумы на всех гипер-прямоугольниках со сторонами степени двойки.
Разреженную таблицу можно применять не только для минимума или максимума. От операции требуется только ассоциативность (\(a ∘ (b ∘ c) = (a ∘ b) ∘ c\)), коммутативность (\(a ∘ b = b ∘ a\)) и идемпотентность (\(a ∘ a = a\)). Например, её можно применять для нахождения \(\gcd\).
Если операция не идемпотентна, то для нахождения её результата можно действовать так: возьмём самый длинный упирающийся в левую границу запроса отрезок, прибавим его к ответу, сдвинем указатель на его правый конец и будем так продолжать, пока не обработаем весь запрос целиком.
int sum(int l, int r) { // [l, r)
int res = 0;
for (int d = logn - 1; d >= 0; d--) {
if (l + (1 << d) < r) {
res += t[l][d];
l += (1 << d);
}
}
return res;
}Это работает быстрее, чем, например, дерево отрезков, но тоже асимптотически за \(O(\log n)\), да ещё и с дополнительной памятью. Но есть способ это ускорить.
Мы хотим иметь какую-то структуру, которая может считать функцию \(f\) на отрезке, при том что \(f\) не удовлетворяет условию идемпотентности. Стандартная разреженная таблица тут не подойдёт — в ней нельзя найти \(O(1)\) непересекающихся отрезков.
Сделаем следующее: мысленно построим на массиве дерево отрезков и (уже не мысленно) для каждого его отрезка \([l, r)\) посчитаем \(f\) на всех отрезках от его центрального элемента — то есть от элемента с индексом \(m = \lfloor \frac{l + r}{2} \rfloor\) — до всех остальных элементов \(k \in [l, r)\). Для каждого элемента массива будет \(O(\log n)\) центральных, а значит суммарно на это потребуются те же \(O(n \log n)\) времени и памяти.
Утверждение. Любой запрос \([l, r)\) разбивается на \(O(1)\) непересекающихся предпосчитанных интервалов.
Доказательство. Возьмем самый высокий центральный элемент \(m\), принадлежащий запросу. Его отрезок полностью покрыает запрос — если бы это было не так, то самым высоким был бы не \(m\), а какая-то из его границ . Раз отрезок запроса \([l, r)\) полностью покрыт, и \(m\) лежит внутри него, то \([l, r)\) можно разбить на предпосчитанные \([l, m)\) и \([m, r)\).
Решать задачу мы так и будем: найдём нужный центральный элемент и сделаем два запроса от него.
Сложная часть — найти этот центральный элемент за константное время — станет чуть проще, если мы будем работать только с массивами длины степени двойки и, соответственно, полными деревьями отрезков. Массивы неподходящей длины дополним до ближайшей степени двойки специальным нейтральным элементом, зависящим от самой операции (например, \(0\) для сложения или \(1\) для умножения).
Будем хранить всю структуру (предпосчитанные значения на отрезках) в массиве t[logn][maxn], в котором первым параметром будет уровень в дереве отрезков (число \(d\) для отрезков размера \(2^d\)), а вторым — граница соответствующего интервала (число \(k\)). Этой информации достаточно, чтобы однозначно восстановить отрезок.
Для ответа на запрос нам достаточно найти только уровень нужного центрального элемента. Чтобы научиться делать это эффективно, нам понадобится немного поразмышлять о природе дерева отрезков.
Заметим, что любая вершина \(k\)-того уровня соответствует какому-то отрезку \([l, l + 2^k)\), причём \(l\) делится на \(2^k\). Двоичное представление всех индексов на этом отрезке будет иметь какой-то общий префикс, а последние \(k\) знаков будут различными.
Нам нужно найти уровень нужного центрального элемента — это то же самое, что и уровень наименьшего общего отрезка для элементов \(l\) и \(r\). Используя предыдущий факт, получаем, что искомый уровень будет равен позиции самого значимого бита, который отличается у чисел \(l\) и \(r\). Его можно найти за константное время выражением \(h_{[l,r)]} = \lfloor \log_2 (l \oplus r) \rfloor\), если заранее предпосчитать логарифмы.
Для примера, построим DST для умножения по составному модулю:
const int maxn = (1 << logn);
int a[maxn], lg[maxn], t[logn][maxn];
const int neutral = 1;
int f(int a, int b) {
return (a * b) % 1000;
}
void build(int l, int r, int level = logn - 1) {
int m = (l + r) / 2;
int cur = neutral;
for (int i = m + 1; i < r; i++) {
cur = f(cur, a[i]);
t[level][i] = cur;
}
cur = neutral;
for (int i = m; i >= l; i--) {
cur = f(cur, a[i]);
t[level][i] = cur;
}
if (r - l > 1) {
build(l, mid, level+1);
build(mid, r, level+1);
}
}
int rmq(int l, int r) { // [l, r)
int level = lg[l ^ r];
int res = t[level][l];
// и, если правый отрезок не пустой:
if (r & ((1 << lg[l ^ r]) - 1)))
res = f(res, t[level][r]);
return res;
}TODO: очень вероятно, тут есть баги.